I can’t believe I solved this problem on my own without looking up any reference material, applying the concepts of dynamic programming. Let me walk you through my approach and how I navigated the problem.
Problem Breakdown
Dealing with zeros was particularly tricky, so I had to carefully consider the ways they could create problems. Initially, I thought about the cases where the string cannot be decoded:
- The string cannot be decoded if
s[0] == '0'. - The string cannot be decoded if there are consecutive zeros, for example:
1200034,4353009. - The string cannot be decoded if
!(1 <= stoi(s.substr(i-1, 2)) <= 26)ands[i] == '0'.
Coding the Above Cases
bool decodeable(string &s){
if(s[0]=='0') return false; //Case 1
int i=1;
int len = s.length();
while(i < len){
if(s[i]=='0'){
if(i+1 < len && s[i+1]=='0') return false; //Case II
if(!inRange(s, i-1)) return false; //Case III
}
i++;
}
return true;
}
It requires a helper function inRange(string &s, int &i) to check whether the number from string is between 1-26 or not.
bool inRange(string &s, int pos){
return (stoi(s.substr(pos, 2)) >=1 && stoi(s.substr(pos, 2)) <=26);
}
Now, after doing the preprocessing, I can proceed peacefully without worrying about the edge cases as I know that the string is decodeable. For all the cases where 0 is coming I know it can be paired with the previous char.
Dynamic Programming Approach
After preprocessing, I can proceed without worrying about edge cases, knowing that the string is decodeable. For all cases where 0 appears, I know it can be paired with the previous character.
If the string length is 1, there is only 1 way to decode it.
Base Case: f(1) = 1
We’re looking for f(n), where n represents the length of the string. We’ll start by considering substrings of increasing length, from 1 to n. We know f(1) = 1.
Case Analysis
If s[n-1] == '0', then:
- Edge Case 1: If
n-3 > 0,f(n)would depend onf(n-3). - Edge Case 2: If
n-3 <= 0, it means it was the start of the string; therefore, we will just add 1 since it’s the first case.
If s[n-1] != '0', then there will be two cases:
- Case 1: It can be paired with the previous character, so
f(n)would depend onf(n-3). - Case 2: It cannot be paired with the previous character, so
f(n)would depend onf(n-2).
Edge Case: When n-3 < 0, it means it was the start of the string, so we will just add 1 since it’s the first case.
Consider the following examples to understand the problem:
- “226”
- “11106”
- “1201234”
- “1201”
- “2101”
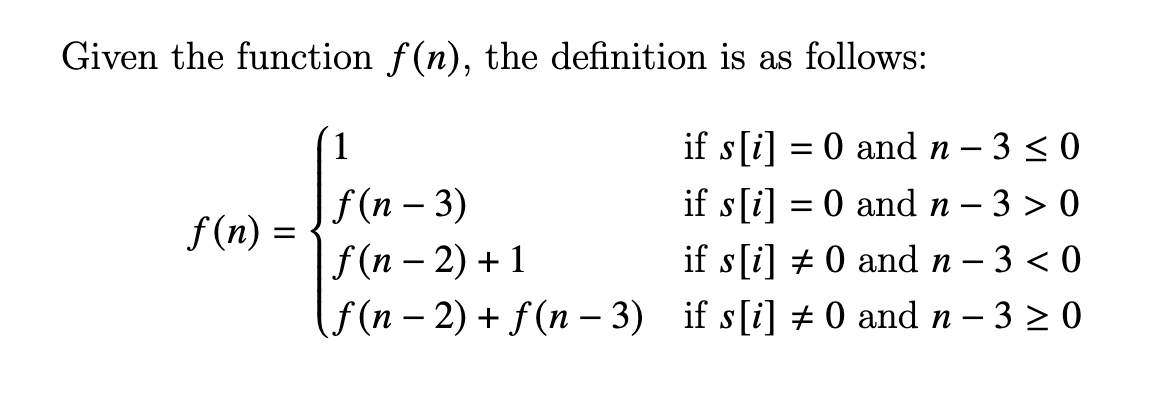
if(s[strLength - 1]=='0'){
//Needs to be paired & can be paired.
if(strLength-3 > 0){
waysToDecode[strLength-1]+=waysToDecode[strLength-3];
}
else waysToDecode[strLength-1] = 1;
}
if(s[strLength - 1]!='0'){
waysToDecode[strLength-1] = waysToDecode[strLength-2]; //No pairing
if(inRange(s, strLength-2)){
//Can be paired
if(strLength-3 >= 0){
waysToDecode[strLength-1]+=waysToDecode[strLength-3];
}
else waysToDecode[strLength-1]+=1;
}
}
Now, we will run the above scenario for all length starting from 2…n
Defining initial values:
vector<int> waysToDecode(s.length(), 0);
waysToDecode[0] = 1; //Base Case
int strLength = 2;
Final Code:
bool inRange(string &s, int pos){
if(s[pos]=='0') return false;
else {
return (stoi(s.substr(pos, 2)) >=1 && stoi(s.substr(pos, 2)) <=26);
}
}
bool decodeable(string &s){
if(s[0]=='0') return false;
int i=1;
int len = s.length();
while(i < len){
if(s[i]=='0'){
if(i+1 < len && s[i+1]=='0') return false;
if(!inRange(s, i-1)) return false;
}
i++;
}
return true;
}
int numDecodings(string s) {
if(!decodeable(s)) return 0;
vector<int> waysToDecode(s.length(), 0);
waysToDecode[0] = 1; //Base Case
int strLength = 2;
while(strLength <= s.length()){
if(s[strLength - 1]=='0'){
//Needs to be paired & can be paired.
if(strLength-3 > 0){
waysToDecode[strLength-1]+=waysToDecode[strLength-3];
}
else waysToDecode[strLength-1] = 1;
}
else{
waysToDecode[strLength-1] = waysToDecode[strLength-2]; //No pairing
if(inRange(s, strLength-2)){
//Can be paired
if(strLength-3 >= 0){
waysToDecode[strLength-1]+=waysToDecode[strLength-3];
}
else waysToDecode[strLength-1]+=1;
}
}
strLength++;
}
return waysToDecode[s.length()-1];
}